少年漫画でバトル系って今のライバルを倒すと、次のまた強烈な敵がで出てきますよね。まぁ、そうしないと連載終わっちゃいますからね。
これを警鐘して”ライバルの強さのインフレ”なんて言われてしまいます。昔の敵が味方になってさらに強力な敵に挑んで行く。そんなのが一時期の少年バトル漫画のセオリーでした。
んで、ふと思ったんですよ。敵の強さってどんな感じで上がっていくのか?倍?階乗?と。そんなこと考えてないで漫画に集中しろって話なんですけれどね。
で、「うん?まてよ、これって”フィボナッチ数列”的に敵が強くなっていっているから上手く行っているのでは?」と。
フィボナッチ数列とは、自分と、一個前(左)を足していく数列(漸化式)で、
簡単に書くと、
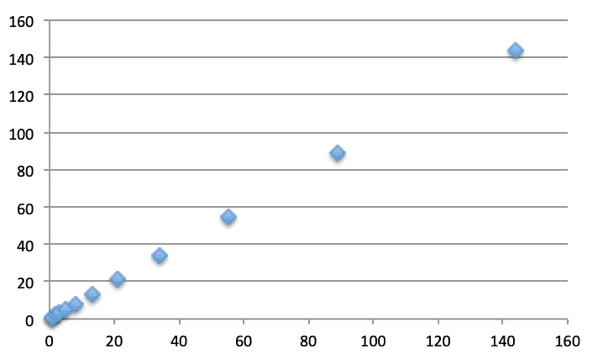
0,1,1,2,3,5,8,13,21,34,55,89,144,233…となっていく数です。
普通にグラフにしていくと、最初は点が密集していて、そこからどんどんと点が離れていく事がわかります。
これを”強さのインフレ”と仮定します。
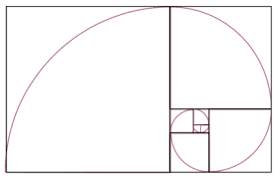
ただ、この”強さのインフレ”、フィボナッチ数列と切っても切り離せない「黄金比」をもとに表現すると、前の敵を味方としてより強い相手と戦うのにちょうど良い比率になっている事がわかります。
インフレするような強い数値(圧倒的な強敵)に見えても、きちんとバランスが取れているのがフィボナッチ数列の特徴です。
最後の的に今までのヒーローが集まって戦う際に、
1(自分)+2(ライバル1)+3(ライバル2)+4(ライバル3) 対 10(最後のライバル)
とかくと等号となりますが、最後のライバルが10ではそんなに強い感じはしませんし、自分が成長していません。そもそもこの場合の10って帳尻を合わせるだけに算出した数値です。
これをフィボナッチ数列で示すと、
1(自分)+1(ライバル1)+2(自分2)+3(ライバル2)+5(自分3)+8(ライバル3) 対 13(最後のライバル)
ちょっと難しいですけれど、ライバルを倒すと仲間になる、もしくはそれ相応の力を手にいれるとなるとこの数値が当てはまります。
これが、強さのインフレに見えて絶妙にバランスを取っている強さなのではないかな?と思ってしまいます。
フィボナッチ数列は非常に面白い数ですし、自然界に実際に存在する数列となっています(花びらの枚数など)
エンジニアの開発手法であるアジャイルにおけるスクラム開発においてはフィボナッチ工数見積なるものもあるそうです。これはアジャイルだから出来る工数見積であり、大規模開発には向かないと思いますが、エンジニア界にもフィボナッチ数列が出てきているんですよね。
非常に面白い数列ですので、色々な単語と組み合わせて検索すると意外な世界が見えるかもしれませんよ。


